http://www.ipai.net.ua/shevchenko-publishing
Задача 1. Козак Вус подарував вам набiр з n цифр (тобто чисел вiд 0 до 9 включно). I хоче дiзнатися у вас: яку максимальну кiлькiсть чисел з них можна скласти так, щоб кожне з них дiлилося на 3 та кожна цифра з набору була використана не бiльше 1 разу. Щоб скласти число, вам потрiбно вибрати будь-які цифри з набору, вибрати їхнiй порядок та скласти число з цих цифр. Звернiть увагу, що ви не зобов’язанi використати всi цифри. Ви ж не можете вiдмовити Вусу? :)
Маленька пiдказка вiд Математичної Сови:
Остача (залишок) вiд дiлення x на число 3 дорiвнює остачi вiд дiлення суми цифр числа x на число 3.
Число a є кратним числу b (тобто a дiлиться на b) лише, якщо остача вiд дiлення числа a на число b дорiвнює 0.
Технічні умови Програма Newnumbers читає з пристрою стандартного введення у першому рядку мiстить одне цiле число n (1 ⩽ n⩽5 · 105) — кiлькiсть цифр. У другому рядку записано n цiлих чисел, кожне з яких має значення вiд 0 до 9 включно. Програма виводить на пристрій стандартного виведення одне ціле число — максимальну кількість чисел кратних 3, що можна скласти з цього набору.
Приклади
Введення
|
Виведення
|
1
0 |
1
|
14
8 8 4 8 1 1 0 0 2 1 9 3 4 1 |
8
|
Зауваження до прикладів
У першому прикладі ми можемо скласти лише одне число 0.
У другому прикладі з цього набору ми можемо скласти максимум 8 чисел. Один iз можливих способів — це скласти такі числа: 0, 0, 48, 9, 3, 21, 81, 84. Невикористаними у нас залишаться цифри 1, 1.
Задача 2. Дано набiр з n цифр вiд 0 до 9 включно. Потрібно дiзнатися, яку максимальну кiлькiсть чисел з них можна скласти так, щоб кожне з них дiлилося на 3 та кожна цифра з набору була використана не бiльше 1 разу. Щоб скласти число, вам потрiбно вибрати будь-які цифри з набору, вибрати їх порядок та скласти число з цих цифр. Звернiть увагу, що ви не зобов’язані використати всi цифри.
Математична підказка:
· Остача (залишок) вiд дiлення x на число 3 дорiвнює остачi вiд дiлення суми цифр числа x на число 3.
· Число a є кратним числу b (тобто a дiлиться на b) лише, якщо остача вiд дiлення числа a на число b дорiвнює 0.
Технічні умови. Програма читає з пристрою стандартного введення у першому рядку одне цiле число n (1 ⩽ n⩽5 · 105) — кiлькiсть цифр. У другому рядку записано n цiлих чисел, кожне з яких має значення вiд 0 до 9 включно. Програма виводить на пристрій стандартного виведення одне цiле число — максимальну кiлькiсть чисел кратних 3, що можна скласти з цього набору.
Приклади
Введення
|
Виведення
|
1
0 |
1
|
14
8 8 4 8 1 1 0 0 2 1 9 3 4 1 |
8
|
Зауваження до прикладів
У першому прикладi ми можемо скласти лише одне число 0.
У другому прикладi з цього набору ми можемо скласти максимум 8 чисел. Один iз можливих способiв — це скласти наступнi числа: 0, 0, 48, 9, 3, 21, 81, 84. Невикористаними у нас залишаться цифри 1, 1.
Математична модель до завдання:
Максимальна кількість чисел обчислюється за формулою
n =p(0=mod3)+min(k(1=mod3); m(2=mod3))+(1/3)*(max(k(1=mod3); m(2=mod3) -min(k(1=mod3); m(2=mod3))
де p(0=mod3) - це кількість цифр, що кратні 3.;
k(1=mod3) -це кількість цифр, що мають вигляд 3х+1;
m(2=mod3)) - це кількість цифр, що мають вигляд 3х+2;
Кодування алгоритму на СІ++
#include <iostream>
#include <cmath>
using namespace std;
int main(){
long long kol, tsifra, ost;
cin >> kol;
long long n = 0, L = 0, m = 0;
for (long long i = 0; i < kol; i++){
cin >> tsifra;
ost = tsifra % 3;
if (ost == 0)
n = n + 1;
else if (ost == 1)
L = L + 1;
else
m = m + 1;
}
long long rez = n + min(L, m) + (max(L, m) - min(L,m))/3;
cout << rez;
}
Кодування алгоритму на мові Рython
var k,l,o,m,n,i,min,max,rez:longint;
begin
readln(n);
k:=0; l:=0; m:=0;
for i:=1 to n do
begin
read(o);
o:=(o mod 3);
case o of
0:k:=k+1;
1:l:=l+1;
2:m:=m+1;
end;
end;
if l>m then begin max:=l; min:=m; end
else begin max:=m; min:=l; end;
rez:=k+min+((max-min) div 3);
write(rez);
endA.
Кодування алгоритму на мові Pascal
var k,l,o,m,n,i,min,max,rez:longint;
begin
readln(n);
k:=0; l:=0; m:=0;
for i:=1 to n do
begin
read(o);
o:=(o mod 3);
case o of
0:k:=k+1;
1:l:=l+1;
2:m:=m+1;
end;
end;
if l>m then begin max:=l; min:=m; end
else begin max:=m; min:=l; end;
rez:=k+min+((max-min) div 3);
write(rez);
end.
Кодування на мові Pascal генератора перевірочних тестів(текстових файлів з даними) до алгоритму:
var f:text;
n,p,i,k,l,m,min,max,a,o,rez,c:longint;
pp:boolean;
begin
read(n);
read(p);
assign(f,'figures.test.20');
rewrite(f);
writeln(f,n);
for i:=1 to n do
begin
pp:=true;
case p of
1:begin while pp do begin a:=random(10); c:=(a mod 3); if c=0 then pp:=false; end; end;
2:begin while pp do begin a:=random(10); c:=(a mod 3); if c=1 then pp:=false; end; end;
3:begin while pp do begin a:=random(10); c:=(a mod 3); if c=2 then pp:=false; end; end;
4:begin while pp do begin a:=random(10); c:=(a mod 3); if ((c=0) or (c=1)) then pp:=false; end; end;
5:begin while pp do begin a:=random(10); c:=(a mod 3); if ((c=0) or (c=2)) then pp:=false; end; end;
6:begin while pp do begin a:=random(10); c:=(a mod 3); if ((c=2) or (c=1)) then pp:=false; end; end;
7:a:=random(10);
end;
write(f,a,' ');
o:=(a mod 3);
case o of
0:k:=k+1;
1:l:=l+1;
2:m:=m+1;
end;
if l>m then begin max:=l; min:=m; end else begin max:=m; min:=l; end;
end;
rez:=k+min+((max-min) div 3);
writeln(f,'');
write(f,rez);
close(f);
write(rez);
end.
Тести для перевірки алгоритму:
Тест 1.
Ввід 4
5 5 8 8
Вивід 1
Тест 2.
Ввід 8
5 5 7 8 8 5 8 4
Вивід 3
Тест 3.
Ввід 16
5 5 7 8 6 8 5 8 4 6 6 3 4 2 8 0
Вивід 9
Тест 4.
Ввід 32
5 5 7 8 8 5 8 4 4 2 8 2 4 7 8 5 4 5 8 8 7 1 8 8 4 7 8 4 5 7 1 7
Вивід 15
НОВА ІНФОРМАЦІЙНА ТЕХНОЛОГІЯ
Технологія обробки інформації та вирішення завдань за допомогою ЕОМ, що спирається на досягнення штучного інтелекту . Основною ідеєю, яка використовується в НІТ, є автоматизація процедури побудови програми, що цікавить користувача, на підставі введеного ним у систему опису постановки задачі на звичному для нього професійною мовою. Таким чином, Н.І.Т. забезпечує можливість спілкування з ЕОМ користувача, який не є професійним програмістом. Для того щоб була реалізована основна ідея Н.І.Т., необхідно, щоб ЕОМ мала інтелектуальним інтерфейсом , базою знань і вирішувачів , тобто була б інтелектуальною системою. Інший рисою Н.І.Т. є розподілений спосіб вирішення завдання, коли користувачі, зайняті вирішенням спільної справи, спілкуються між собою через мережу ЕОМ, електронну пошту та загальну базу знань. До мережі входять також бази даних , з яких користувачі черпають інформацію для вирішення свого завдання.| Всі етапи визначаються поставленим завданням і цілями моделювання. У загальному випадку процес побудови і дослідження моделі можна представити наступною схемою: Перший етап - постановка задачі включає в себе стадії: опис завдання, визначення мети моделювання, аналіз об'єкта.Опис задачі Задача формулюється на звичайній мові. За характером постановки всі завдання можна розділити на дві основні групи. До першої групи можна віднести завдання, в яких потрібно дослідити, як зміняться характеристики об'єкта при деякому впливі на нього, «що буде якщо?... ». Наприклад, що буде, якщо магнітний диск покласти поруч з магнітом? У завданнях, що відносяться до другої групи, потрібно визначити, яке треба зробити вплив на об'єкт, щоб його параметри задовольняли деякому заданому умові, «як зробити, щоб?.. ». Наприклад, як треба побудувати освітній процес в сучасній школі, щоб дітям було цікаво вчитися? Визначення мети моделювання |
| На цій стадії необхідно серед багатьох характеристик (параметрів) об'єкта виділити істотні. Ми вже говорили про те, що для одного і того ж об'єкта при різних цілях моделювання істотними будуть вважатися різні властивості. |
| Наприклад, якщо ви будуєте модель яхти для участі в змаганнях моделей суден, то в першу чергу вас будуть цікавити її судноплавні характеристики. Ви будете вирішувати завдання «як зробити, щоб ...?» |
| Визначення мети моделювання дозволяє чітко встановити, які дані є вихідними, що потрібно отримати на виході і якими властивостями об'єкта можна знехтувати. Таким чином, будується словесна модель задачі.Аналіз об'єкта передбачає чітке виділення об'єкта, що моделюється і його основних свойств.Второй етап - формалізація завдання пов'язаний зі створенням формалізованої моделі, Тобто моделі, збережені на будь-яких формальній мові. Наприклад, дані перепису населення, представлені у вигляді таблиці або діаграми - це формалізована модель. |
| У загальному сенсі формалізація - це приведення істотних властивостей і ознак об'єкта моделювання до обраної формі. |
| Третій етап - розробка комп'ютерної моделі починається з вибору інструменту моделювання, іншими словами, програмного середовища, в якій буде створюватися і досліджуватися модель. Від цього вибору залежить алгоритм побудови комп'ютерної моделі, а також форма його подання. У середовищі програмування це програма, Написана на відповідній мові. У прикладних середовищах (електронні таблиці, СУБД, графічних редакторах і т. Д.) Це послідовність технологічних прийомів, Що призводять до вирішення завдання. Слід зазначити, що одну і ту ж задачу можна вирішити, використовуючи різні середовища. Вибір інструмента моделювання залежить, в першу чергу, від реальних можливостей, як технічних, так і матеріальних. Четвертий етап - комп'ютерний експеримент включає дві стадії: тестування моделі та проведення дослідження. тестування моделі
дослідження моделі До цієї стадії комп'ютерного експерименту можна переходити тільки після того, як тестування моделі пройшло успішно, і ви впевнені, що створена саме та модель, яку необхідно досліджувати. П'ятий етап - аналіз результатів є ключовим для процесу моделювання. Саме за підсумками цього етапу приймається рішення: продовжувати дослідження або закінчити. Якщо результати не відповідають цілям поставленого завдання, значить, на попередніх етапах були допущені помилки. В цьому випадку необхідно коригувати модель, Тобто повертатися до одного з попередніх етапів. процес повторюється до тих пір, поки результати комп'ютерного експерименту не відповідатимуть цілям моделювання. |
Моделювання обєктів, що утворюють множину Каталана
Числа Каталана
- Математика для програмістів
Розглянемо послідовність чисел: 1 , 1, 2 , 5 , 14 , 42 , 132 , 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 34305966540, 3430596, 3630, 3430596, 3630, 3430596, 3630, 3430596, 3430596, 3430596, 3430596, 3630, 3430596, 3630, 3430596, 3630, 3430596, 3630, 3430596, 3630594, 34305963640, 3430596364 4861946401452, ...
Це послідовність чисел Каталана, які дивним чином спливають в самих різних комбінаторних задачах. На жаль, вони випадають з розгляду типовий шкільної програми, але впевнений, що будь-який фахівець комп'ютерних наук повинен бути знайомий з ними.
Саме число Каталана виражається формулою C(n) = (2n)! / n!(n+1)!, де знак оклику, як зазвичай, позначає факторіал. Початок послідовності виглядає так: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 ...
Англійська Вікіпедія стверджує, що відомо, як мінімум 66 різних конструкцій, які призводять до появи чисел Каталана. Ось деякі з них:
Для кожної з цих конструкцій можна або по індукції, або реккурентное співвідношеннями довести, що число відповідних об'єктів виражається числом Каталана. Не буду зупинятися на цих доказах - їх можна знайти в підручниках з дискретної математики. Також є деякі чудові співвідношення, які можна отримати, використовуючи деякі зі згаданих побудов. Але це вимагає написання громіздких формул, чого хотілося б уникнути. Зараз цікавіше інше - невже збіг всіх цих кількостей для абсолютно різних речей випадковість?
Звичайно ж ні. Зв'язок цих конструкцій набагато глибше. Можна побудувати взаимнооднозначное відповідність між цими об'єктами і деякі з таких відповідностей я спробую продемонструвати. Крім простої цікавості це має і деяку практичну цінність. Наприклад, завдання про генерацію всіх бінарних дерев (рішення якої в лоб неочевидно) можна звести до набагато більш простого завдання про генерацію дужкових послідовностей.
Дуже легко побудувати відповідність між Дужковий послідовностями і монотонними шляхами в квадраті. Читаючи дужкову послідовність зліва направо, будемо будувати шлях, почавши з лівого нижнього кута, - для кожної дужки що намалюємо горизонтальний відрізок, для закривається дужки - вертикальний.
Так як в послідовності було рівне число відкриваються і закриваються дужок, то шлях в підсумку закінчиться в правому верхньому куті, а той факт, що кожна дужка варто наперед відповідної їй закривається дужки (адже послідовність - правильна) гарантує нам, що шлях не перейде в верхню половину квадрата. Очевидно, що це побудова оборотно і з кожного монотонного шляху можна отримати дужкову послідовність.
На наведеному малюнку відповідні дужки і відрізки відзначені одним кольором. Добре помітно, що відрізки, відповідні одній парі дужок «бачать один одного»:

В якості другої задачі побудуємо відповідність між правильними Дужковий послідовностями і таблицями юнгам 2xn. Тут теж все просто. Пронумеруємо дужки зліва направо. Якщо дужка відкривається, то відповідне їй число пишемо в верхній рядок. Якщо закривається, то в - нижню. Так як i перша дужка завжди стоїть лівіше i-ой закривається, то число відповідне відкривається скобці буде менше числа, відповідного закриває. А значить, верхнє число в таблиці виявиться менше нижнього в тій же колонці, тобто з правильної скобочной послідовності ми отримали таблицю Юнга. Це побудова також можна зупинити, а значить отримано взаємно-однозначна відповідність.

Тепер займемося бінарними деревами. Дуже легко побачити відповідність між бінарними деревами і розстановками дужок у виразі з однорідними операціями, але це дає дещо інші послідовності. Для прив'язки бінарних дерев до правильних Дужковий послідовностям треба скористатися дещо іншим підходом. Скористаємося стандартним обходом дерева і пронумеруємо вершини (корінь приймемо за 0) в порядку обходу. Тепер, якщо при переході до числа I ми спустилися від батьків до дитини, то на i-е місце ставимо відкривається дужку. В іншому випадку ставимо закривається.

Дерево - бінарне, тому у кожного вузла є сусід. А значить, спустившись до дитини і поставивши відкривається дужку, ми рано чи пізно доберемося до його сусіда і поставимо закривається дужку. Це гарантує правильність отриманої послідовності. Побудова легко звернути і взявши за основу дужкову послідовність отримати бінарне дерево.
Зауважимо, що якщо в скобочной послідовності n пар то відповідне дерево має n + 1 лист.
Для побудови відповідності між тріангуляції багатокутника найпростіше використовувати бінарне дерево. На цей раз ми Занумеруем в ньому все листя зліва направо (інші вузли пометим буквами). Для тріангуляції візьмемо багатокутник, в якому вершин на одну більше, ніж листя в дереві. Одну зі сторін цього багатокутника відзначимо, як стартову, а решта Занумеруем (для наочності - проти годинникової стрілки).
Далі виконуємо наступну процедуру - якщо дві вершини дерева сусідні, то відповідні сторони багатокутника «стягнемо» діагоналлю, яку позначимо тією буквою, якої позначений батько цієї пари вузлів в дереві. Далі продовжуємо процедуру «стягування» поки від багатокутника не залишиться єдиний стартовий відрізок.
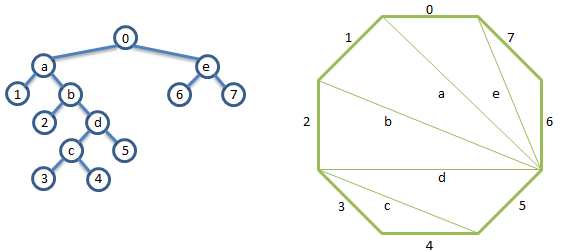
Як можна помітити три сторони кожного трикутника в отриманому розбитті відповідають одному батьківському вузлу і двом його нащадкам. Тому, якщо взяти два різних дерева, то вийде два різних розбиття.
Ну і на закінчення приведу табличку, в якому зображено відповідність об'єктів для третього числа Каталана.

Саме число Каталана виражається формулою C(n) = (2n)! / n!(n+1)!, де знак оклику, як зазвичай, позначає факторіал. Початок послідовності виглядає так: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 ...
Англійська Вікіпедія стверджує, що відомо, як мінімум 66 різних конструкцій, які призводять до появи чисел Каталана. Ось деякі з них:
- Правильні дужкові послідовності - набори відкриваються і закриваються дужок, в яких кожній відкривається скобці відповідає закривається. Число можливих послідовностей з фіксованим числом пар дужок виражається числом Каталана. Наприклад, 14 правильних послідовностей з чотирьох пар дужок:
(((()))), ((() ())), ((()) ()), ((())) (), (() ( ())), (() () ()), (() ()) (),
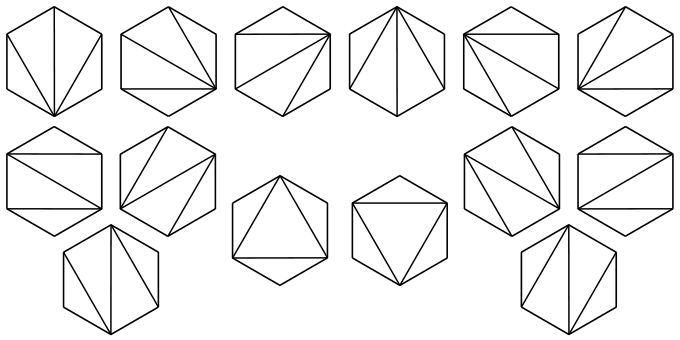
(()) (()), (()) () (), () ((())), () (() ()), () (()) (), () () (()), () () () () - Двійкові дерева - дерева, з кожного вузла яких (крім листя) виходить рівно дві гілки. Кількість бінарних дерев із заданим числом листя - число Каталана. На малюнку представлені п'ять дерев з 4 листям в кожному.

Такі дерева вже обговорювалися на Хабре - Будь-які дерева. Число неізоморфних дерев із заданим числом вершин також дорівнює числу Каталана. Такі дерева теж обговорювалися
- Монотонні шляху в квадраті - маршрути з лівого нижнього кута квадрата в правий верхній, які йдуть по лініях сітки вгору або вправо і не заходять вище діагоналі. На малюнку всі такі шляхи для квадрата 3x3.

- Тріангуляції багатокутника. Кількість різних тріангуляцій опуклого багатокутника діагоналями дорівнює числу Каталана.
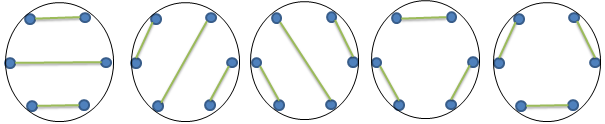
- Розбиття вершин багатокутника на пари. Парне число точок на окружності можна об'єднати в пари непересічними хордами. Число способів таких об'єднань також дорівнює числу Каталана.
- Таблиця Юнга - прямокутник, заповнений послідовними числами так, щоб вони зростали у всіх рядках і шпальтах. Число таблиць Юнга розміром 2xn також виражається числом Каталана.

Для кожної з цих конструкцій можна або по індукції, або реккурентное співвідношеннями довести, що число відповідних об'єктів виражається числом Каталана. Не буду зупинятися на цих доказах - їх можна знайти в підручниках з дискретної математики. Також є деякі чудові співвідношення, які можна отримати, використовуючи деякі зі згаданих побудов. Але це вимагає написання громіздких формул, чого хотілося б уникнути. Зараз цікавіше інше - невже збіг всіх цих кількостей для абсолютно різних речей випадковість?
Звичайно ж ні. Зв'язок цих конструкцій набагато глибше. Можна побудувати взаимнооднозначное відповідність між цими об'єктами і деякі з таких відповідностей я спробую продемонструвати. Крім простої цікавості це має і деяку практичну цінність. Наприклад, завдання про генерацію всіх бінарних дерев (рішення якої в лоб неочевидно) можна звести до набагато більш простого завдання про генерацію дужкових послідовностей.
відповідність 1
Дуже легко побудувати відповідність між Дужковий послідовностями і монотонними шляхами в квадраті. Читаючи дужкову послідовність зліва направо, будемо будувати шлях, почавши з лівого нижнього кута, - для кожної дужки що намалюємо горизонтальний відрізок, для закривається дужки - вертикальний.
Так як в послідовності було рівне число відкриваються і закриваються дужок, то шлях в підсумку закінчиться в правому верхньому куті, а той факт, що кожна дужка варто наперед відповідної їй закривається дужки (адже послідовність - правильна) гарантує нам, що шлях не перейде в верхню половину квадрата. Очевидно, що це побудова оборотно і з кожного монотонного шляху можна отримати дужкову послідовність.
На наведеному малюнку відповідні дужки і відрізки відзначені одним кольором. Добре помітно, що відрізки, відповідні одній парі дужок «бачать один одного»:

відповідність 2
В якості другої задачі побудуємо відповідність між правильними Дужковий послідовностями і таблицями юнгам 2xn. Тут теж все просто. Пронумеруємо дужки зліва направо. Якщо дужка відкривається, то відповідне їй число пишемо в верхній рядок. Якщо закривається, то в - нижню. Так як i перша дужка завжди стоїть лівіше i-ой закривається, то число відповідне відкривається скобці буде менше числа, відповідного закриває. А значить, верхнє число в таблиці виявиться менше нижнього в тій же колонці, тобто з правильної скобочной послідовності ми отримали таблицю Юнга. Це побудова також можна зупинити, а значить отримано взаємно-однозначна відповідність.

відповідність 3
Тепер займемося бінарними деревами. Дуже легко побачити відповідність між бінарними деревами і розстановками дужок у виразі з однорідними операціями, але це дає дещо інші послідовності. Для прив'язки бінарних дерев до правильних Дужковий послідовностям треба скористатися дещо іншим підходом. Скористаємося стандартним обходом дерева і пронумеруємо вершини (корінь приймемо за 0) в порядку обходу. Тепер, якщо при переході до числа I ми спустилися від батьків до дитини, то на i-е місце ставимо відкривається дужку. В іншому випадку ставимо закривається.

Дерево - бінарне, тому у кожного вузла є сусід. А значить, спустившись до дитини і поставивши відкривається дужку, ми рано чи пізно доберемося до його сусіда і поставимо закривається дужку. Це гарантує правильність отриманої послідовності. Побудова легко звернути і взявши за основу дужкову послідовність отримати бінарне дерево.
Зауважимо, що якщо в скобочной послідовності n пар то відповідне дерево має n + 1 лист.
відповідність 4
Для побудови відповідності між тріангуляції багатокутника найпростіше використовувати бінарне дерево. На цей раз ми Занумеруем в ньому все листя зліва направо (інші вузли пометим буквами). Для тріангуляції візьмемо багатокутник, в якому вершин на одну більше, ніж листя в дереві. Одну зі сторін цього багатокутника відзначимо, як стартову, а решта Занумеруем (для наочності - проти годинникової стрілки).
Далі виконуємо наступну процедуру - якщо дві вершини дерева сусідні, то відповідні сторони багатокутника «стягнемо» діагоналлю, яку позначимо тією буквою, якої позначений батько цієї пари вузлів в дереві. Далі продовжуємо процедуру «стягування» поки від багатокутника не залишиться єдиний стартовий відрізок.

Як можна помітити три сторони кожного трикутника в отриманому розбитті відповідають одному батьківському вузлу і двом його нащадкам. Тому, якщо взяти два різних дерева, то вийде два різних розбиття.
замість епілогу
Ну і на закінчення приведу табличку, в якому зображено відповідність об'єктів для третього числа Каталана.

Немає коментарів:
Дописати коментар