06.12.2021 - 12.12.2021 Створення в MS Excel статистичних таблиць

 

06.12.2021 - 12.12.2021

 

Тема: Створення в MS Excel  статистичних таблиць з даними та формулами, з фільтрами, з діаграмами. Налаштування лінії тренду для вибірки

 

Теоретична частина

 

Статистичні дані подають у вигляді таблиць, діаграм, графіків.

 

За допомогою ранжирування ряду, таблиці і графічних ілюстрацій отримують по­чаткові відомості про закономірності статистичного ряду даних.

Більш якісний статистичний аналіз дозволяють зробити такі статистичні характеристи­ки ряду даних, як мода, медіана, середнє значення випадкової величини, які називають­ся центральними тенденціями вибірки.

Мода Мо - це те значення випадкової величини, яке зустрічається найчастіше (в при­кладі 1: Мо = 3).

Медіана Ме - це число, яке поділяє навпіл упорядковану за зростанням сукупність (ряд) усіх значень випадкової величини:

·        якщо кількість чисел у ряду непарна, то медіана - це число, що записане посередині;

·        якщо кількість чисел у ряду парна, то медіана - це середнє арифметичне двох чисел, що стоять посередині (в прикладі 1: Ме = 3).

[Запам'ятаємо ]

Середнім значенням х випадкової величини х називається середнє арифметичне всіх її значень:

X_m=(x₁+ х₂, ..., х_n)/n  , де x₁, х₂, ..., х_n  - значення, яких набуває випадкова величина, n - кількість значень випадкової величини.

Приклад 1

Для з'ясування рівня знань учнів 9-х класів у школах мікрорайону склали спеціальну контрольну роботу з шести завдань. У школах мікрорайону навчається 710 дев'ятиклас­ників, з яких випадковим чином відібрали 50 учнів (обсяг вибірки n), і в алфавітному спис­ку цих учнів біля кожного прізвища після проведення контрольної роботи проставили кількість правильно розв'язаних задач. Вийшов ряд даних (статистичні дані):

4; 2; 0; 6; 2; 3; 4; 3; 3; 0; 1; 5; 2; 6; 4; 3; 3; 2; 3; 1; 3; 3; 2; 6; 2; 2; 4; 3; 3; 6; 4; 2; 0; 3; 3; 5; 2; 1; 4; 4; 3; 4; 5; 3; 2; 3; 1; 6; 2; 2.

Щоб зручніше було аналізувати інформацію, розташували ці числа в порядку їх зростан­ня (ранжирування ряду даних):

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 6; 6; 6.

Для кращого сприйняття і полегшення подальшого аналізу результатів, їх подають у виг­ляді таблиці, яка встановлює зв'язок між впорядкованим рядом статистичних даних і відповідними їм частотами m_і (або відносними частотами v_i)

 

Кількість правильно розв'язаних задач, хі	0	1	2	3	4	5	6
Частота, mi	3	4	12	15	8	3	5
Відносна частота, vi , (у %)	6	8	24	30	16	6	10

Перевірка: 1) додаємо всі частоти ті і одержуємо обсяг вибірки n = 50;

2) додаємо всі відносні частоти v_i, і одержуємо 100%. Отже, таблиця заповнена правильно.

 

Для графічного подання даних на основі цієї таблиці можна побудувати різні типи діаграм частот (або відносних частот):

1) лінійна діаграма являє собою набір відрізків, що спираються на певні значення випадко­вої величини х_і (статистичні дані), а висоти їх дорівнюють відповідним частотам m_і (або віднос­ним частотам v_i,) цих величин:

 

 2) стовпчаста діаграма складається з окремих стовпців - прямокутників, основи яких вибирають довільної ширини на значеннях випадкової величини х_n а висоти дорівнюють відповідним частотам m_i. (або відносним частотам v_i) цих величин:

 

3) для побудови кругової діаграми круг розбивається на сектори, центральні кути яких пропорційні відносним частотам v_i, обчисленим для кожного значення випадкової величини:

 

 

Крім діаграм для графічного представлення результатів використовують полігони частот (або відносних частот).

Полігон частот являє собою ламану, відрізки якої послідовно з'єднують точки з коорди­натами (х_i; v_i), де х_і - значення випадкової величини, а v_i. - відповідні їм частоти.

 

 

Увага!  

У випадках, коли в статистичному ряді даних однакові значення зустрічаються рідко, а кількість різних варіантів досить велика, для обробки даних будують інтервальний ряд. Для побудови такого ряду спочатку знаходять серед даних найбільше значення і найменше значення і визначають розмах ряду даних. Потім весь інтервал значень ряду даних розби­вається на декілька (5 -10) однакових інтервалів і визначається, яка кількість даних по­трапляє в кожний інтервал.

 

Приклад  2

Для з'ясування, чи зручно розташована школа в мікрорайоні, провели опитування учнів. Вибраних випадковим чином 100 учнів (обсяг вибірки n) запитали, скільки часу кожен з них витрачає на дорогу від дому до школи.

У результаті опитування отримали ряд даних (статистичні дані):

40, 18, 31, 45, 24, 30, 37, 15, 39, 34, 48, 25, 30, 7, 27, 52, 43, 38, 47, 8, 21, 40, 32, 53, 45, 54, 35, 28, 32, 12, 26, 35, 48, 19, 33, 26, 17, 30, 42, 22, 53, 28, 42, 36, 23, 10, 34, 46, 16, 29, 35, 52, 41, 32, 21, 39, 55, 25, 29, 8, 36, 44, 26, 55, 34, 19, 42, 54, 27, 10, 45, 20, 31, 50, 18, 9, 41, 14, 38, 40, 23, 49, 33, 15, 24, 46, 36, 28, 32, 37, 51, 20, 29, 47, 33, 27, 41, 22, 39, 40.

Найбільше значення серед даних - 55, найменше - 7, розмах вибірки: 55 - 7 = 48. Вибере­мо довжину інтервалу, наприклад: 48:6 = 8. За початок кожного інтервалу прийнято брати значення, розташоване на півінтервалу лівіше найменшого значення в ряду, тобто 7 - 4 = 3. Тоді границі інтервалів: 3, 11, 19, 27, 35, 43, 51, 59. Визначимо, скільки значень потрапить у кожний інтервал, тобто частоту попадання в даний інтервал. Побудуємо таблицю:

 

Інтервал часу (у хв), х,	3-11	11-19	19-27	27-35	35-43	43-51	51-59
Частота, m	6	8	17	24	23	13	9

Для інтервального ряду використовують спеціальне графічне зображення - гістогра­му частот (або відносних частот).

Гістограма частот являє собою ступінчасту фігуру, що складається із з'єднаних між со­бою стовпців-прямокутників; основою кожного стовпця слугує проміжок значень випадко­вої величини, а висотою - частота, з якою зустрічається ця величина.

 

Приклад 3.

Учні 9-го класу проходили тестування з математики, де оцінка виставлялася за 100-бальною шкалою. Середня оцінка 10 учнів становила 81 бал. Якою має бути середня оцінка реш­ти 20 учнів класу, щоб середня оцінка всього класу дорівнювала 85 балам?

Розв'язання.

Нехай оцінка одного учня х₁ балів, другого - х₂ балів, тридцятого – х₃₀ балів. Тоді се­редня оцінка 10 учнів становить 81 бал: (x₁+ х₂+...+х₁₀):10 = 81. 

Cередня оцінка решти 20 учнів нехай буде z:  (x₁₁+ х₁₂+...+х₃₀):20 = z , а середня оцінка всього класу дорівнює 85 балам: (x₁+ х₂+...+х₃₀):30 = 85.Одержуємо систему з трьох рівнянь:

x₁+ х₂+...+х₁₀ = 810;  x₁₁+ х₁₂+...+х₃₀ = 20z; x₁+ х₂+...+х₃₀= 2550

з якої визначаємо z:

810 + 20z = 2550,

20z = 2550 - 810,

20z =1740,

z = 87.

Відповідь: середня оцінка решти 20 учнів класу становить 87.

 

Узагальнення поняття про статистику

 

Математична статистика та її методи

Розділ математики, в якому вивчаються та досліджуються кіль­кісні характеристики масових явищ, називається математичною статистикою (останнє слово від латинського зіаіиз — стан). Мате­матична статистика вивчає математичні методи систематизації, об­робки та використання статистичних даних для наукових і практич­них висновків, а також аналізує результати, одержані за допомогою моделей, створених методами теорії ймовірностей.

Статистику поділяють на описову і пояснювальну.

Описова статистика займається добором кількісної інформації, необхідної або цікавої для суспільства. Наприклад, спортивна інфор­мація, середньорічна температура в певному регіоні, середній рівень заробітної плати тощо. Для цього обробляються та узагальнюються великі масиви даних.

Пояснювальна статистика з отриманих статистичних результа­тів робить висновки, будує прогнози.

Предметом вивчення статистики є: кількість і склад населення, тру­дові ресурси суспільства, їхній розподіл та використання, національне багатство, матеріальний достаток населення, виробництво і розподіл суспільного продукту, освіта, культура, охорона здоров'я тощо.

Складові статистичного методу: масове спостереження, групуван­ня даних, обчислення середніх величин, побудова графіків. При цьо­му першим етапом статистичного дослідження є статистичне спосте­реження. Найбільш поширене вибіркове спостереження, коли з усієї сукупності роблять відбір одиниць спостереження. Вся сукупність називається генеральною, а сукупність одиниць відібраних для спо­стереження, називається вибіркою.

Вибірка поділяється на  випадкову вибірку, коли відбір здійснюється із сукупності же­ребкуванням;

Основною задачею математичної статистики є розробка методів одержання науково обґрунтованих висновків про поведінку масових явищ і процесів за результатами спостережень. Умови  такої задачі можна розчленити на дві.

Першою задачею є розробка методів збору і групування статистичних даних, одержаних у результаті спостережень, опрацювання статистичних звітів чи даних у результаті спеціально поставлених експериментів.

Друга задача полягає в розробці методів аналізу статистичних даних залежно від мети. Сюди належать:

а) оцінка ймовірності події; знаходження функції розподілу випадкової величини; оцінка залежності випадкової величини від  випадкових величин тощо;

б) перевірка статистичних гіпотез, зроблених вище припущеннях.

Висновки за допомогою методів математичної статистика зроблені за зібраними статистичними даними, повинні правильно відображати загальні ймовірнісні характеристики процесу, що досліджує­ться.

 

Поняття тренду та лінії тренду

 

Тренд (статистика) - це загальна тенденція при різнонаправленому русі, визначена загальною спрямованістю змін показників часового ряду.

Тренд (економіка) - це напрямок переважного руху показників.

 

Лінії тренду - елемент апарату технічного аналізу, який використовується, зокрема, для виявлення тенденцій зміни цін на різних видах бірж.

Лінії тренду є геометричним відображенням середніх значень аналізованих показників, отримане за допомогою будь-якої математичної функції. Вибір функції для побудови лінії тренду зазвичай визначається характером зміни даних у часі.

Виділяється три типи трендів:

·         «Бичачий» (зростаючий) — ціни ростуть (від порівняння з биком, який піднімає рогами вгору);

·         «Ведмежий» (падаючий) — ціни падають (від порівняння з ведмедем, який б'є лапою вниз);

·         «Флет» (бічний) — ціни знаходяться в цінових діапазонах. Як правило, консолідація відбувається перед наступним зростанням або падінням.

 

 

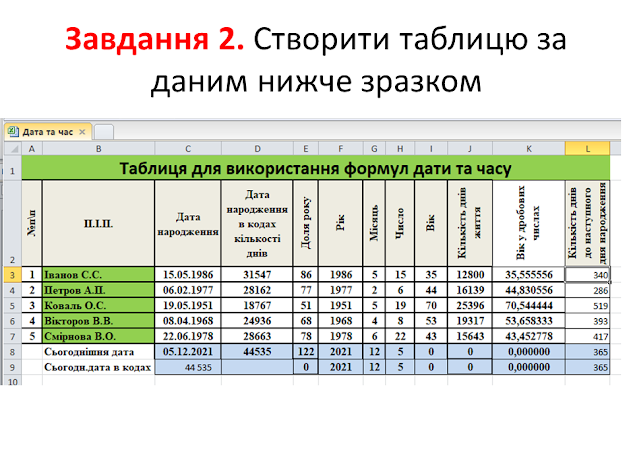
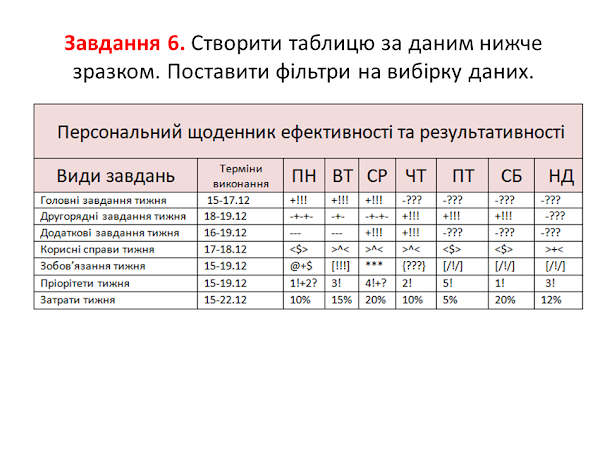
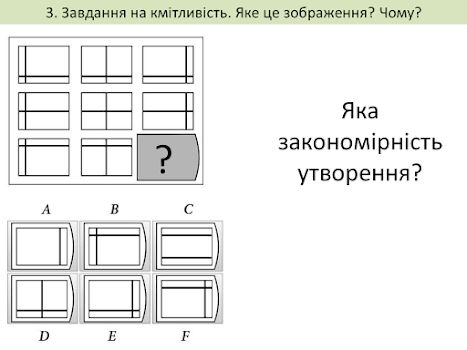
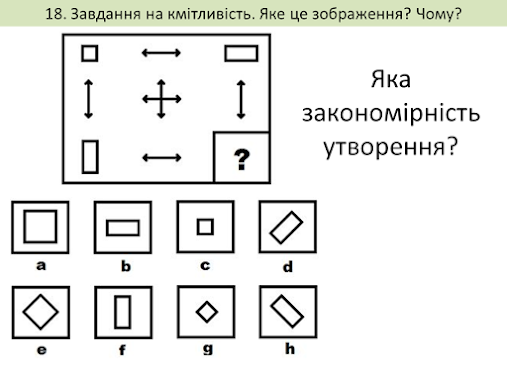
Практична частина

 

Результати виконання практичної частини надіслати на електронну адресу:  vinnser@gmail.com

Завдання на розвиток кмітливості. Інтелектуальна уява